Products Category
- FM Transmitter
- 0-50w 50w-1000w 2kw-10kw 10kw+
- TV Transmitter
- 0-50w 50-1kw 2kw-10kw
- FM Antenna
- TV Antenna
- Antenna Accessory
- Cable Connector Power Splitter Dummy Load
- RF Transistor
- Power Supply
- Audio Equipments
- DTV Front End Equipment
- Link System
- STL system Microwave Link system
- FM Radio
- Power Meter
- Other Products
- Special for Coronavirus
Products Tags
Fmuser Sites
- es.fmuser.net
- it.fmuser.net
- fr.fmuser.net
- de.fmuser.net
- af.fmuser.net ->Afrikaans
- sq.fmuser.net ->Albanian
- ar.fmuser.net ->Arabic
- hy.fmuser.net ->Armenian
- az.fmuser.net ->Azerbaijani
- eu.fmuser.net ->Basque
- be.fmuser.net ->Belarusian
- bg.fmuser.net ->Bulgarian
- ca.fmuser.net ->Catalan
- zh-CN.fmuser.net ->Chinese (Simplified)
- zh-TW.fmuser.net ->Chinese (Traditional)
- hr.fmuser.net ->Croatian
- cs.fmuser.net ->Czech
- da.fmuser.net ->Danish
- nl.fmuser.net ->Dutch
- et.fmuser.net ->Estonian
- tl.fmuser.net ->Filipino
- fi.fmuser.net ->Finnish
- fr.fmuser.net ->French
- gl.fmuser.net ->Galician
- ka.fmuser.net ->Georgian
- de.fmuser.net ->German
- el.fmuser.net ->Greek
- ht.fmuser.net ->Haitian Creole
- iw.fmuser.net ->Hebrew
- hi.fmuser.net ->Hindi
- hu.fmuser.net ->Hungarian
- is.fmuser.net ->Icelandic
- id.fmuser.net ->Indonesian
- ga.fmuser.net ->Irish
- it.fmuser.net ->Italian
- ja.fmuser.net ->Japanese
- ko.fmuser.net ->Korean
- lv.fmuser.net ->Latvian
- lt.fmuser.net ->Lithuanian
- mk.fmuser.net ->Macedonian
- ms.fmuser.net ->Malay
- mt.fmuser.net ->Maltese
- no.fmuser.net ->Norwegian
- fa.fmuser.net ->Persian
- pl.fmuser.net ->Polish
- pt.fmuser.net ->Portuguese
- ro.fmuser.net ->Romanian
- ru.fmuser.net ->Russian
- sr.fmuser.net ->Serbian
- sk.fmuser.net ->Slovak
- sl.fmuser.net ->Slovenian
- es.fmuser.net ->Spanish
- sw.fmuser.net ->Swahili
- sv.fmuser.net ->Swedish
- th.fmuser.net ->Thai
- tr.fmuser.net ->Turkish
- uk.fmuser.net ->Ukrainian
- ur.fmuser.net ->Urdu
- vi.fmuser.net ->Vietnamese
- cy.fmuser.net ->Welsh
- yi.fmuser.net ->Yiddish
What is Used to Represent Gain?
The Bel is Used to Represent Gain
In its simplest form, an amplifier’s gain is a ratio of output over input. Like all ratios, this form of gain is unitless. However, there is an actual unit intended to represent gain, and it is called the bel.
As a unit, the bel was actually devised as a convenient way to represent power loss in telephone system wiring rather than gain in amplifiers. The unit’s name is derived from Alexander Graham Bell, the famous Scottish inventor whose work was instrumental in developing telephone systems. Originally, the bel represented the amount of signal power loss due to resistance over a standard length of electrical cable. Now, it is defined in terms of the common (base 10) logarithm of a power ratio (output power divided by input power):
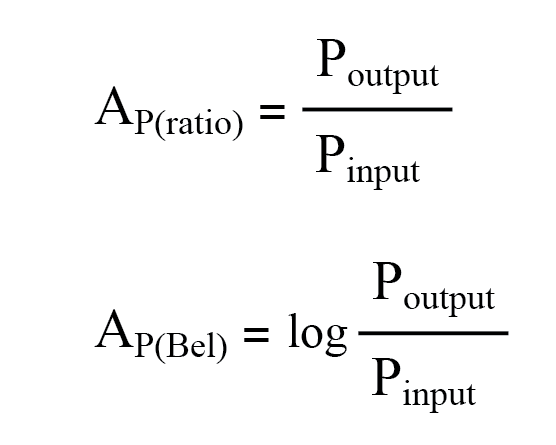
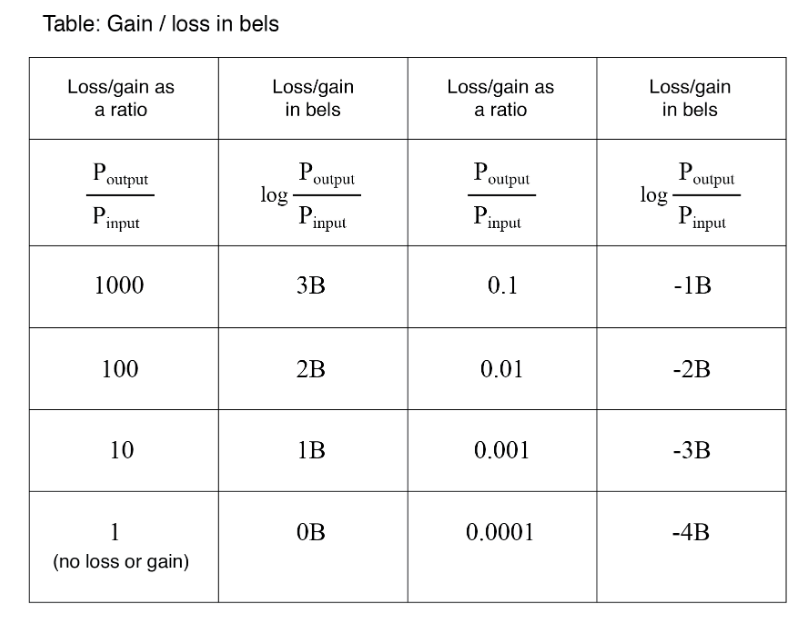
The Bel is Nonlinear
Because the bel is a logarithmic unit, it is nonlinear. To give you an idea of how this works, consider the following table of figures, comparing power losses and gains in bels versus simple ratios:
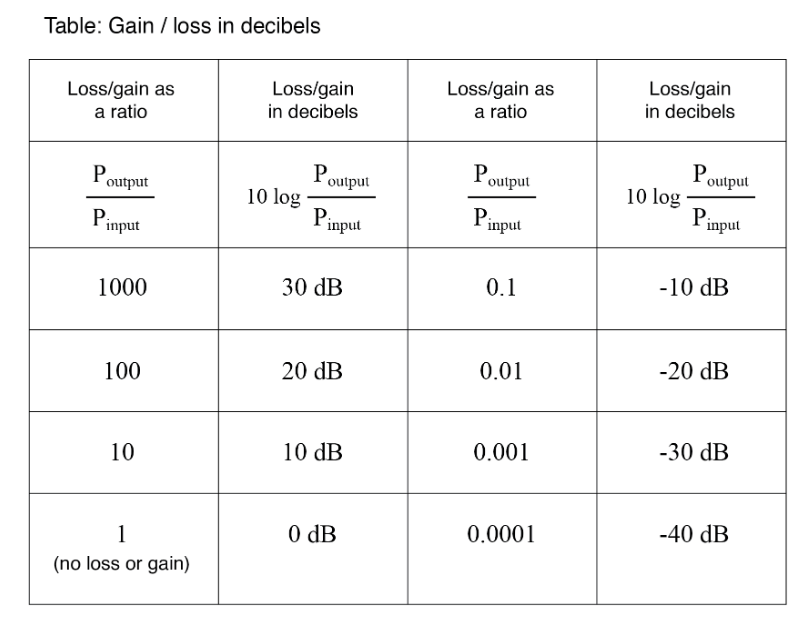
It was later decided that the bel was too large of a unit to be used directly, and so it became customary to apply the metric prefix deci (meaning 1/10) to it, making it decibels, or dB. Now, the expression “dB” is so common that many people do not realize it is a combination of “deci-” and “-bel,” or that there even is such a unit as the “bel.” To put this into perspective, here is another table contrasting power gain/loss ratios against decibels:
Human Hearing is Nonlinear
Human hearing is highly nonlinear: in order to double the perceived intensity of a sound, the actual sound power must be multiplied by a factor of ten. Relating telephone signal power loss in terms of the logarithmic “bel” scale makes perfect sense in this context: a power loss of 1 bel translates to a perceived sound loss of 50 percent, or 1/2. A power gain of 1 bel translates to a doubling in the perceived intensity of the sound.
Other Logarithmic Scale Examples: Richter Scale and Chemical pH
Richter Scale
An almost perfect analogy to the bel scale is the Richter scale used to describe earthquake intensity: a 6.0 Richter earthquake is 10 times more powerful than a 5.0 Richter earthquake; a 7.0 Richter earthquake 100 times more powerful than a 5.0 Richter earthquake; a 4.0 Richter earthquake is 1/10 as powerful as a 5.0 Richter earthquake, and so on.
Chemical pH
The measurement scale for chemical pH is likewise logarithmic, a difference of 1 on the scale is equivalent to a tenfold difference in hydrogen ion concentration of a chemical solution. An advantage of using a logarithmic measurement scale is the tremendous range of expression afforded by a relatively small span of numerical values, and it is this advantage which secures the use of Richter numbers for earthquakes and pH for hydrogen ion activity.
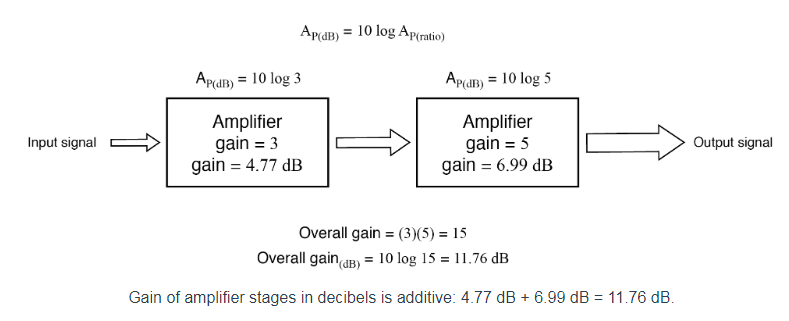
Using the Bel to Express System Gains and Losses
Another reason for the adoption of the bel as a unit for gain is for simple expression of system gains and losses. Consider the last system example (figure above) where two amplifiers were connected tandem to amplify a signal. The respective gain for each amplifier was expressed as a ratio, and the overall gain for the system was the product (multiplication) of those two ratios:
Overall gain = (3)(5) = 15

Gains using Decibels
Recalculating for decibels rather than bels, we notice the same phenomenon. (Figure below)
To those already familiar with the arithmetic properties of logarithms, this is no surprise. It is an elementary rule of algebra that the antilogarithm of the sum of two numbers’ logarithm values equals the product of the two original numbers. In other words, if we take two numbers and determine the logarithm of each, then add those two logarithm figures together, then determine the “antilogarithm” of that sum (elevate the base number of the logarithm—in this case, 10—to the power of that sum), the result will be the same as if we had simply multiplied the two original numbers together.
This algebraic rule forms the heart of a device called a slide rule, an analog computer which could, among other things, determine the products and quotients of numbers by addition (adding together physical lengths marked on sliding wood, metal, or plastic scales).
Given a table of logarithm figures, the same mathematical trick could be used to perform otherwise complex multiplications and divisions by only having to do additions and subtractions, respectively. With the advent of high-speed, handheld, digital calculator devices, this elegant calculation technique virtually disappeared from popular use. However, it is still important to understand when working with measurement scales that are logarithmic in nature, such as the bel (decibel) and Richter scales.
Conversion of Decibels and Unitless Ratio
When converting a power gain from units of bels or decibels to a unitless ratio, the mathematical inverse function of common logarithms is used: powers of 10, or the antilog.
Converting decibels into unitless ratios for power gain is much the same, only a division factor of 10 is included in the exponent term:
Example: Power into an amplifier is 1 Watt, the power out is 10 Watts. Find the power gain in dB.
AP(dB) = 10 log10(PO / PI) = 10 log10 (10 /1) = 10 log10 (10) = 10 (1) = 10 dB
AP(dB) = 20 = 10 log10 AP(ratio) 20/10 = log10 AP(ratio) 1020/10 = 10log10 (AP(ratio)) 100 = AP(ratio) = (PO / PI)
Because the bel is fundamentally a unit of power gain or loss in a system, voltage or current gains and losses don’t convert to bels or dB in quite the same way. When using bels or decibels to express a gain other than power, be it voltage or current, we must perform the calculation in terms of how much power gain there would be for that amount of voltage or current gain.
For a constant load impedance, a voltage or current gain of 2 equates to a power gain of 4 (22); a voltage or current gain of 3 equates to a power gain of 9 (32). If we multiply either voltage or current by a given factor, then the power gain incurred by that multiplication will be the square of that factor. This relates back to the forms of Joule’s Law where power was calculated from either voltage or current, and resistance:

Thus, when translating a voltage or current gain ratio into a respective gain in terms of the bel unit, we must include this exponent in the equation(s):
The same exponent requirement holds true when expressing voltage or current gains in terms of decibels:
However, thanks to another interesting property of logarithms, we can simplify these equations to eliminate the exponent by including the “2” as a multiplying factor for the logarithm function. In other words, instead of taking the logarithm of the square of the voltage or current gain, we just multiply the voltage or current gain’s logarithm figure by 2 and the final result in bels or decibels will be the same:

The process of converting voltage or current gains from bels or decibels into unitless ratios is much the same as it is for power gains:
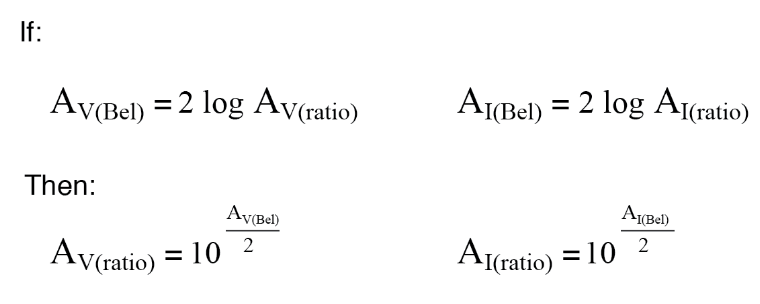
Here are the equations used for converting voltage or current gains in decibels into unitless ratios:

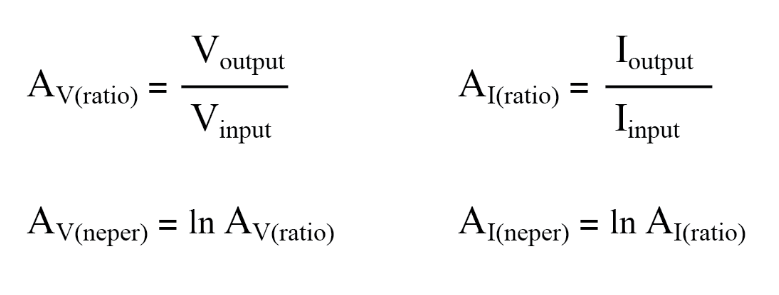
While the bel is a unit naturally scaled for power, another logarithmic unit has been invented to directly express voltage or current gains/losses, and it is based on the natural logarithm rather than the common logarithm as bels and decibels are. Called the neper, its unit symbol is “Np; though, lower-case “n” may be encountered.
Example: The voltage into a 600 Ω audio line amplifier is 10 mV, the voltage across a 600 Ω load is 1 V. Find the power gain in dB.
A(dB) = 20 log10(VO / VI) = 20 log10 (1 /0.01) = 20 log10 (100) = 20 (2) = 40 dB
Example: Find the voltage gain ratio AV(ratio) = (VO / VI) for a 20 dB gain amplifier having a 50 Ω input and out impedance.
AV(dB) = 20 log10 AV(ratio) 20 = 20 log10 AV(ratio) 20/20 = log10 AP(ratio) 1020/20 = 10log10 (AV(ratio)) 10 = AV(ratio) = (VO / VI)
A Review of the Decibel
Gains and losses may be expressed in terms of a unitless ratio, or in the unit of bels (B) or decibels (dB). A decibel is literally a deci-bel: one-tenth of a bel.The bel is fundamentally a unit for expressing power gain or loss. To convert a power ratio to either bels or decibels, use one of these equations:
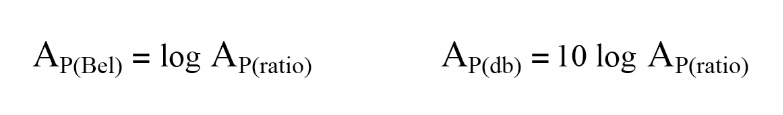
When using the unit of the bel or decibel to express a voltage or current ratio, it must be cast in terms of an equivalent power ratio. Practically, this means the use of different equations, with a multiplication factor of 2 for the logarithm value corresponding to an exponent of 2 for the voltage or current gain ratio:
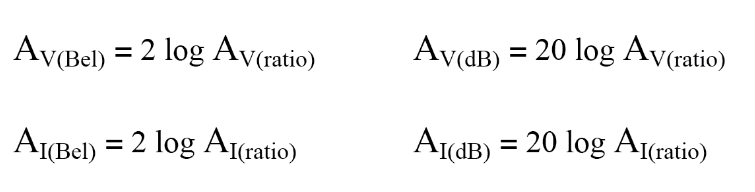
To convert a decibel gain into a unitless ratio gain, use one of these equations:

A gain (amplification) is expressed as a positive bel or decibel figure. A loss (attenuation) is expressed as a negative bel or decibel figure. Unity gain (no gain or loss; ratio = 1) is expressed as zero bels or zero decibels.
If you would like to build a radio station, boost your FM radio transmitter or need any other FM equipment, please feel free to contact us: [email protected].

